Linear Regression with One Variable

model Representation

 

以上篇博文中的房价预测为例，从图中依次来看，m表示训练集的大小，此处即房价样本数量；x表示输入变量或feature（特征），此处即房子面积；y是输出变量或目标变量，此处即房子价格。（x，y）是训练集中的一个样本，如图中加上右上角（i）表示训练集中第i个样本。

 

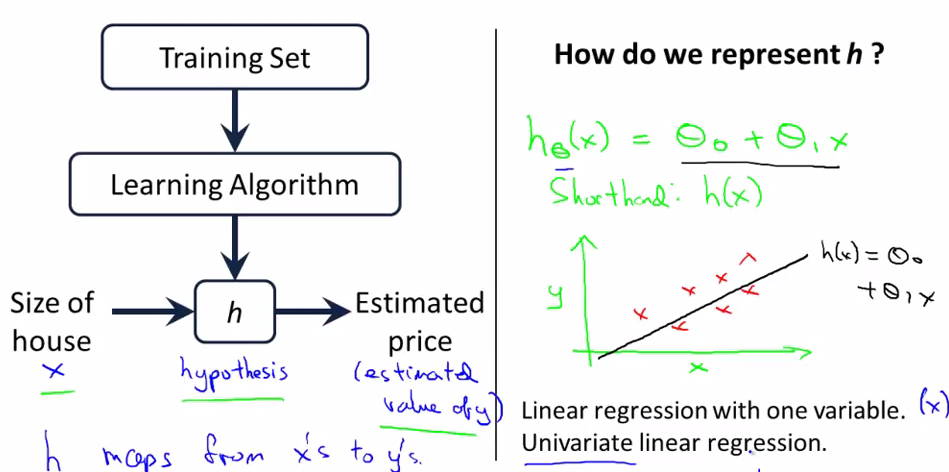
上图是机器学习的一个简单流程，我们通过对Training Set（训练集）使用Learning Algorithm 来训练出一个hypothesis函数（hypothesis是机器学习一直沿用下来的一个用语，不用纠结其具体含义），这样使用该函数就可以预估房价了。

hypothesis有很多种形式，上图是线性回归的一张二维坐标系图示，为了简单，途中只有一个输入变量x，纵轴y是输出变量，图中红色的叉是训练集中的点，黑色的直线就是我们的hypothesis函数，可以看到，该直线并没有经过所有的点，所以预估出来的值h(x)就会跟y只存在误差，这就涉及到下面要讲的cost函数。

cost function

cost function实际上就是求方差，预测值与实际值之间的。主要是用来寻找合适的参数。

 

如上图所示，为了简单起见，这里的theta只设置两个，并用一条直线来拟合。右上角的公式的意思就是寻找使cost function最小的theta值。注意，按照方差的定义来解释，公式中应该是1/m，这里除以2纯粹是为了计算导数方便，之所以可以这样改，是因为虽然方差值变化了，但是据此公式求出的theta值没有影响，比如从含一百个不同的整数的数组挑出最小的那个数的坐标，和把这一百个数除以2后再求得到的结果是一样的。

 

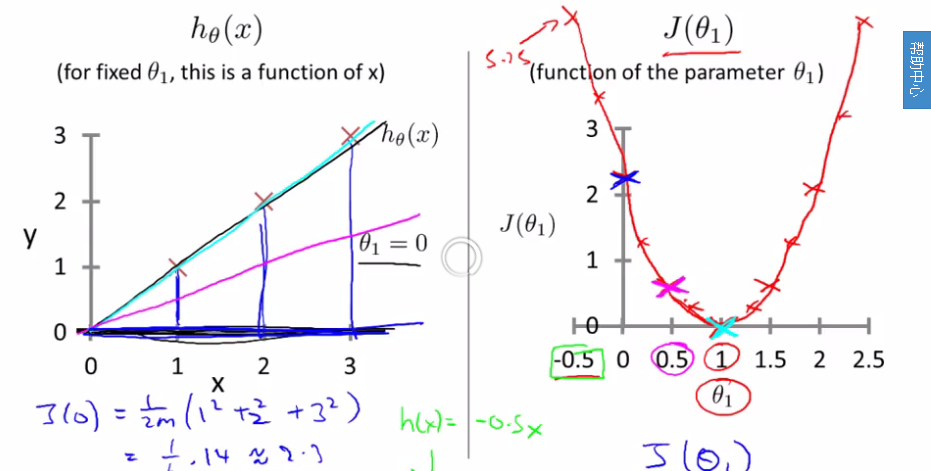
上图左侧直线是预测函数，右侧cost function。图中的 是实际值。右侧说明，当theta为1时，cost最低，此时的拟合就可认为是最好的拟合，当然上图中的点恰好的在直线上，实际场景中这种现象是不可能的。

 

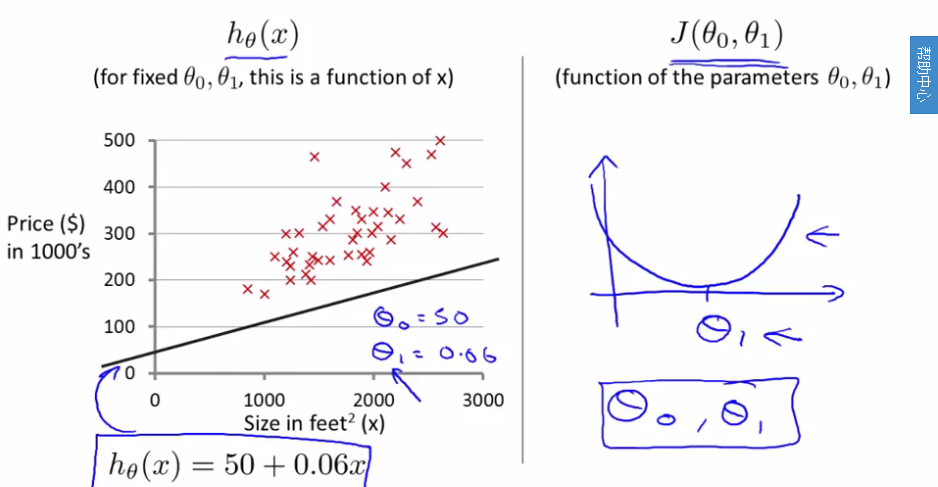
现在给一个具体的预测函数，如上图左侧所示，此时我们重新使用两个theta值。右侧是只有一个theta1的cost function，下图是两个theta的cost function，是一个三维图像。

 

由于多维图像表示麻烦，之后的教程都已轮廓图来表示，以上图为例，用多个平行底面的平面切割图像，会得到很多闭合的线，将这些线投射到底面形成的图像将在之后使用。

 

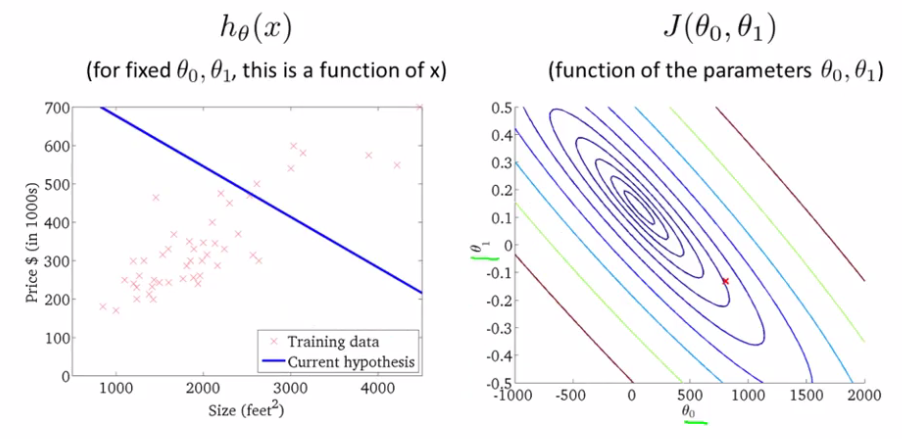
稍作分析可知，左侧图形同一条线上的cost值是相同的，最小值则出现在中心那个圈上。

Gradient Descent

问题描述：

 

将两个theta初始化为0，然后不断改变二者的值来降低cost大小，直到达到我们满意的精度为止。

 

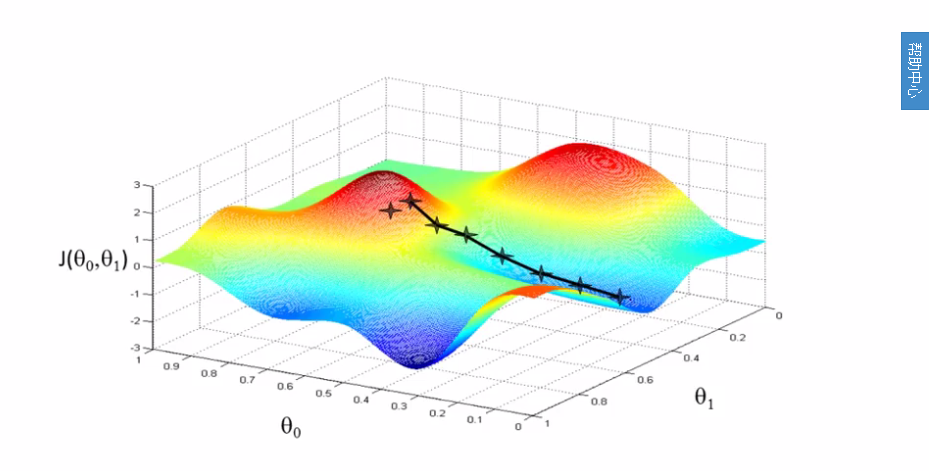
形象的来看，可以将上图看做一座山，将梯度下降看成一个下山的过程，由于存在局部最优解，上图下山的路径是由好几条的。图中只显示了一条路径。

 

上图是梯度下降过程，正如图中所说，我们通过不断修改theta的值，直到收敛。“：=”是赋值，“=”相当于c语言中的“==”，是比较。Learning rate是学习速率，在下山那个例子中讲，就是下山的步子大小。需要注意的是，theta的值需要同时更新，像左侧那样。

 

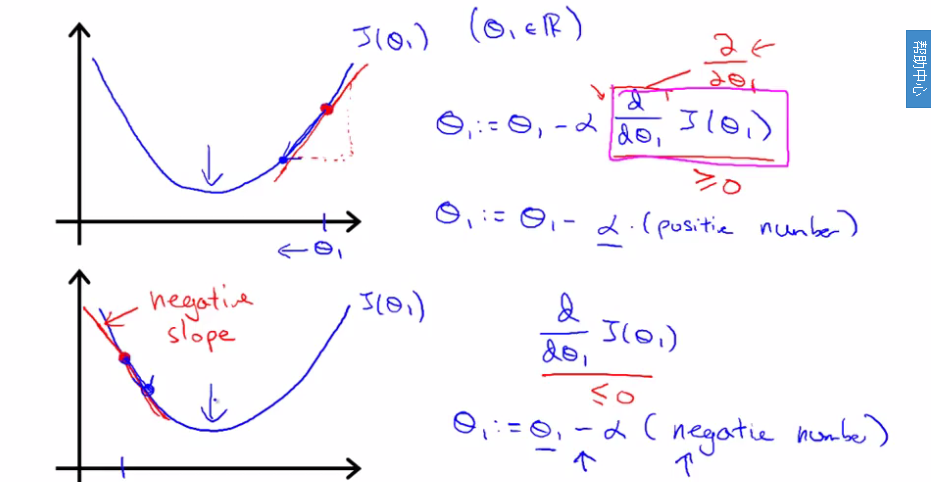
上图解释了更新theta的原理，求cost function最小值就是求其导数为零的时候。

 

上图是学习速率的解释，该值太小，收敛就很慢，即第一个图那样，太大则无法收敛，即第二个图那样。

Gradient Descent For Linear Regression

 

将之前的总结下，应用在一起。关键是上述导数项。

 

例子中有两个theta，要对其求偏导数，即上图的公式。

这里提到一个batch gradient Descent（批量梯度算法）就是指每步都将所有训练集加入运算。